
자연계에서 발생하는 현상을 재현하거나 그 현상을 규명하는 방법에는 크게 두 가지로 분류할 수 있다. 첫째는 실험적 방법으로 그 현상을 규명하기 위하여 실험장치를 제작하고 필요한 측정장비를 이용한다. 다른 하나는 이론적인 분석으로 그 현상을 지배하는 원리와 조건을 보통 미분방정식이라 불리는 수학적 표현식에 대한 해답을 이론적으로 푸는 것이다.
→ 부끄럽지만 전산역학 강의를 들을 때 프로젝트를 진행하면서 정확하게 깨달았습니다. simulation만 돌리는 것은 아무 의미도 없는 것...
어쨌든, 예를 들어 폭설이 내려 지붕이 무너져 내렸을 때 얼마나 튼튼한 골재와 구조를 선택해야 하는지, 덤프트럭 위에 이상하게 생긴 모자를 붙이고 안 붙이고의 차이 등이 궁금할 때가 있습니다. 이것을 실제 크기로 제작을 해서 결과값을 얻을 수도 있지만 비용이 많이 듭니다. 그래서 크기를 줄여 제작한 다음 동일한 환경에서 실험을 할 수도 있습니다. 또한 이보다 더 저렴한 비용으로 결과값을 알 수 있는 방법은 이론적인 방법(역학적 계산)으로 얻는 방법입니다. 실험적 방법으로 계산해도 되고 이론적인 방법으로 계산해도 됩니다. 그것은 자유. 하지만 이 방법들은 당연하게도 장단점이 있습니다.
이 두 가지 방법은 각기 장점과 단점을 지니고 있다. 전자의 경우에는 대상이 되는 현상을 직접 눈으로 볼 수 있지만 단점으로는 실험장치를 구성하기 위해 많은 돈과 시간 그리고 노력이 요구된다. 또한 실험적으로 재현할 수 없는 경우도 종종 있다. 후자의 경우는 실험장치를 필요로 하지 않기 때문에 재정적인 부담은 적지만, 실제 자연현상을 규명하기에는 많은 한계가 따른다. 왜냐하면 대부분의 자연 형상은 그 대상이 되는 물체의 형상이 매우 복잡하기 때문에 수학적으로 풀 수가 없다. 우리가 손으로 푸는 미분방정식은 거의 대부분 형상이 매우 복잡하기 때문에 수학적으로 풀 수가 없다. 우리가 손으로 푸는 미분방정식은 거의 대부분 형상이 매우 단순한 문제에만 국한되어 있기 때문이다. 따라서 이론적인 방법의 단점을 극복하기 위한 방법이 수치해석이다. 수치해석은 수학적 표현식에 대한 정확한 해답을 푸는 것이 아니라, 컴퓨터를 이용하여 근사해(approximate solution)를 구하는 방법이다.

→ 실험적 방법과 이론적 방법의 장점과 단점을 설명하고 있습니다. 앞에 지붕의 예시를 이어서 설명하자면(구조해석은 거의 안정화되었지만), 실험으로 지붕이 받는 응력과 변형률을 계산할 때 모형을 제작해서 만들면 비용이 저렴합니다. 하지만 실제와 동일한 환경으로 만들수록 비용이 증가할 수밖에 없습니다. 그래서 이론적인 방법으로 계산하게 됩니다. (사실 실험할 때도 이론 값을 계산해야 합니다.) 하나의 트러스를 계산할 때는 쉽지만 트러스의 구조가 복잡해지고 지붕의 모양이 난해해진다면 계산하기 정말 힘들어질 것이고 손으로 풀기 힘들어지겠죠? 그래서 나온 방법이 컴퓨터로 계산하는 방법인 수치해석입니다. 수치해석 방법으로 응력과 변형률을 계산하는 것입니다. 컴퓨터는 정확하게 곡선을 그리며 계산할 수 없습니다. 잘개 쪼갠 후(미분) 그 점들을 이어주어야 하는데 그 계산법이 바로 수치해석입니다. 하지만 점과 점 사이를 이어주는 것이며 정확한 값과 오차가 생기게 됩니다. 이것 또한 수치해석의 장단점이 되겠습니다...
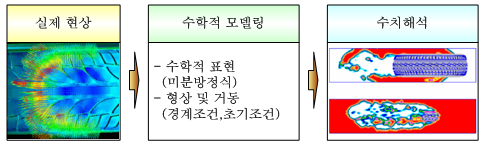
모든 수치해석 기법의 공통점은 미분방정식을 행렬 방정식으로 변환하고 이 행렬 방정식을 컴퓨터를 이용하여 푼다는 점과 그 답이 정답이 아니라 근사해라는 점이다. 미분방정식을 행렬 방정식으로 전환하는 방법에는 여러 가지 기법이 있는데, 어떻게 행렬식으로 전환시키느냐에 따라 수치해석 기법이 분류된다. 유한요소법(finite element method)은 대상 물체의 영역을 다수의 유한요소(finite element)로 나누어 효과적으로 행렬 방정식으로 전환시키는 기법이다.
→ 수치해석 수업을 듣다 보면 여러 가지 수치적 계산법이 있습니다. 예를 들어 룽게-쿠타, 오일러, 심프슨 등의 방법이 있죠. 이때 유한요소법이라는 단어가 잠깐 언급이 되는데 간단하게 설명하자면 지붕 트러스의 막대를 어떤 모양으로 잘게 쪼개는 법입니다. 이렇게 작게 쪼갤 때 컴퓨터는 실제값을 그대로 쪼갤 수가 없습니다. 그러나 비슷하게 쪼개고자 해서 만든 방법들이 바로 룽게쿠타, 오일러 등... 이 되고 이런 것들을 통틀어 수치해석이라고 합니다.

쉽게 설명하고자 했는데 이미 책에서부터 쉽게 설명해주고 있어서 똑같은 말을 반복하게 되네요.ㅋㅋ 그래도 한 번 더 적으며 공부하게 되니까 머릿속이 정리되고 좋네요.
본 글은 'midasNFX CAE용어해설집'을 참고하고 있으며 공부용 블로그이므로 어떠한 상업적 의도가 없음을 밝힙니다. 또한 CAE에 관심있는 기계공학과 학생이 개인적으로 공부하며 작성하는 것이므로 정확하지 않을 수 있습니다. 혹여나 내용이 알맞지 않은 부분이 있다면 지적 부탁드립니다.
'# CAE 용어 공부하기 > CAE 입문자 _ 일반 용어' 카테고리의 다른 글
| [CAE 입문용어] 동해석(Dynamic Analysis) (0) | 2019.07.05 |
|---|---|
| [CAE 입문용어] 정해석(Static Analysis) (0) | 2019.07.04 |
| [CAE 입문용어] 후처리기(Post-Processor) (0) | 2019.07.03 |
| [CAE 입문용어] 솔버(Solver), 처리기(Processor) (0) | 2019.07.02 |
| [CAE 입문용어] 전처리기(Pre-Processor) (0) | 2019.07.01 |



