
자연계의 모든 현상은 본질적으로 비선형적 거동을 나타낸다.
선형과 비선형의 구분은 현상을 일으키는 입력값과 현상이란 출력 값이 비례관계에 있느냐 그렇지 않느냐로 판단된다. 만일 x축을 현상을 일으키는 입력값을 그리고 y축을 출력 값으로 하여 하나의 그래프로 표현하였을 때, 선형적인 현상은 직선으로 표현되는 반면, 비선형적 현상은 더 이상 직선으로 표현되지 않는다. 비선형 거동에서는 변형, 온도, 속도 등과 같이 구하고자 하는 값이 구하기 위해 필요한 여러 가지 계수들에게 영향을 미친다는 점이다.
→ 자연계의 모든 현상은 비선형적 거동을 나타냅니다. 나무젓가락을 부러뜨렸을 때조차도 비선형적 거동이라고 하죠. 위의 그래프에 있는 식 F=Ku 식은 유한요소 해석의 구조강성행렬이 생각납니다. 선형 해석은 행렬 방정식에서 강성행렬(stiffness matrix) [K]가 물체의 거동 {u}와 무관한 일정한 값을 가진다고 말했었죠. 그래서 u값을 구하려면 강성행렬을 역행렬로 취해 쉽게 구할 수 있습니다. 하지만 비선형 해석을 여러 가지 조건(계수)이 섞이고 얽혀 많은 계산을 수행해야 합니다. 선형이란 말 그대로 직선으로 이루어져 있는 값입니다. 그래서 어떠한 값을 변할 때 값 또한 비례적으로 증감하는 것을 알 수 있습니다. 하지만 비선형이라는 것은 선형적이지 않다는 것(non)이기 때문에 한눈에 예측하기 어렵습니다. F=Ku를 행렬로 생각한다면, 선형 해석은 K가 독립적이어서 u값을 쉽게 구할 수 있지만 비선형 해석은 K와 u가 연결되어있는, 독립적이지 않으며 같은 미지수를 가지고 있다고 생각하시면 될 것 같습니다. K 안에 미지수 x, u안에 미지수 x.
→ 위의 그래프에서 비선형곡선만을 살펴보았을 때 두 개의 선이 갈라지는 부분을 항복점이라고 합니다. 이 점을 기준으로 전은 선형적, 후는 비선형적으로 나타나 있습니다.
비선형 문제는 푸는 방법에 있어서도 선형문제와 큰 차이가 있다. 선형문제의 경우에는 계산에 포함되어 있는 여러 가지 계수들이 구하고자 하는 값에 영향을 받지 않기 때문에 단 한번의 계산으로 답을 찾을 수 있다. 반면, 비선형의 경우에는 우선 여러 가지 계수값들을 미리 추정하여 구하고자 하는 값을 계산한다. 그 다음 계산된 값으로 여러 가지 계수값들을 수정한 후 구하고자 하는 값을 다시 계산하는 반복과정을 거쳐야 한다. 따라서 비선형 문제를 푸는데 걸리는 계산 시간은 대략적으로 선형문제를 풀기 위해 걸리는 시간에 반복계산 회수를 곱한 만큼 비례적으로 증가한다.

→ 선형과 비선형 비교 그래프입니다. 비선형은 힘과 변위의 관계에서 기울기가 힘과 변위의 "함수"로 표현된다고 나와있습니다. 앞에서 설명했듯이 하나의 고유값이 아니라 미지수가 포함된 함수라는 것이죠. 그래서 그 미지수의 값이 변할 때마다 기울기는 매번 다시 계산이 되는 것이고 해석시간이 몇 배로 오래 걸릴 수밖에 없습니다.

공학문제에 있어 비선형성은 크게 재료비선형(material nonlinear), 기하비선형(geometry nonlinear), 그리고 경계비선형(boundary nonlinear)으로 대별된다. 재료비선형은 탄성계수, 열전달률, 점성거동(viscosity) 등과 같은 재료 고유의 물성값이 일정하지 않고 변형, 온도, 속도 등과 같이 구하고자 하는 거동과 더불어 변하는 경우이다. 기하비선형은 대상 물체의 형상과 크기가 구하고자 하는 변수와 더불어 변하는 경우이다. 마지막으로 경계비선형은 물체 경계영역의 크기, 형상 그리고 경계조건(boundary condition)이 구하고자 하는 변수와 더불어 변하는 경우이다.
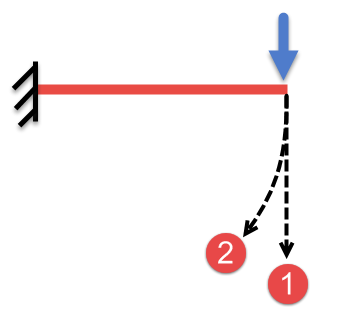
→ 재료 비선형은 재료 자체가 비선형 재료일 때 발생합니다. 탄소성, 점탄성, 점소성 재료 특성을 가지는 재료 물성에 기인한 비선형입니다. 인장응력에서 시편을 잡아 늘릴 때 잡아 늘리는 힘에 의해 재료가 변형하게 된다면 그것을 재료비선형이라고 합니다. 아무리 잡아늘리고 열을 주고 해도 변하지 않는다면 그것은 선형재료라고 합니다. 이처럼 재료의 모양이 변하기에 그래프의 곡선이 선형이지 않게 되는 것입니다.

→ 기하 비선형은 하중을 받았을 때 변형이 치수에 비해 매우 커질 때 발생합니다. 어렸을 때 자주 먹던 마이쮸를 예로 들겠습니다. 마이쮸를 잡아서 늘리면 쭉 늘어나는 것을 본 적이 있을겁니다. 그 마이쮸의 모양이 변하게 되면 마이쮸가 가지고 있던 고유의 강성이 변하게 됩니다. 마이쮸가 쭉 늘어나서 10cm가 늘어났다?! 와 이거 크게 변했네! 해서 대.변.형....ㅋㅋ 기하급수적으로 크게 변하는 것을 기하 비선형이라고 합니다. 대표적으로 대변형, 대변위, 대회전, 좌굴 등이 있습니다. 전산역학에서 트러스 해석을 하는데 얇고 긴 막대를 이용하여 계산하는 거라 좌굴해석을 이용했던 것이 생각나네요. 얇고 긴 막대를 휘었을 때 많이 휘어질 거라 예상된다면 기하비선형을 계산해보심 될 것입니다.

→ 경계비선형(접촉/경계비선형)은 말 그대로 두 물체가 있을 때 접촉하는 부분에서 발생합니다. 접촉이 발생하게 되면 초기에 적용되던 하중조건과 구속조건이 바뀌게 되기 때문입니다. 예를 들어 다른 재료를 띄고 있는 정육면체 2개가 떨어져 있습니다. 따로따로 눌렀을 때는 고유의 해석 결과가 나오지만 두 정육면체를 붙인 후 누른다면 겹쳐있는 부분에서 마찰 등의 문제로 인해 결과값이 다르게 나옵니다. 그렇기 때문에 실험을 해서 결과값을 얻지 않는 이상 접촉해석 혹은 경계비선형으로 해석을 수행해야 합니다.
이처럼 비선형에서도 다양한 조건에서 해석을 수행할 수 있습니다. 이와 관련해 자세한 설명은 개별적으로 포스팅 할 때 더 좋은 예시를 들고 오도록 노력하겠습니다.
본 글은 'midasNFX CAE용어해설집'을 참고하고 있으며 공부용 블로그이므로 어떠한 상업적 의도가 없음을 밝힙니다. 또한 CAE에 관심 있는 기계공학과 학생이 개인적으로 공부하며 작성하는 것이므로 정확하지 않을 수 있습니다. 혹여나 내용이 알맞지 않은 부분이 있다면 지적 부탁드립니다.
'# CAE 용어 공부하기 > CAE 입문자 _ 일반 용어' 카테고리의 다른 글
| [CAE 입문용어] 접촉해석(Contact Analysis) (0) | 2020.01.10 |
|---|---|
| [CAE 입문용어] 비선형해석(Nonlinear Analysis) (0) | 2020.01.09 |
| [CAE 입문용어] 모드 해석(Modal Analysis) (0) | 2019.07.19 |
| [CAE 입문용어] 열해석(Thermal Analysis) (0) | 2019.07.18 |
| [CAE 입문용어] 선형해석(Linear Analysis) (0) | 2019.07.16 |



